MATLAB快速入门(三)
一.简介
本篇参考官方入门文档编写
前提准备:
- MATLAB
二. 快速入门(三)
1. 帮助和文档
所有 MATLAB® 函数都有辅助文档,这些文档包含一些示例,并介绍函数输入、输出和调用语法。从命令行访问此信息有多种方法:
使用
doc命令在单独的窗口中打开函数文档。1
doc mean
在键入函数输入参数的左括号之后暂停,此时命令行窗口中会显示相应函数的提示(函数文档的语法部分)。
1
mean(
使用
help命令可在命令行窗口中查看相应函数的简明文档。1
help mean
点击帮助图标  即可访问完整的产品文档。
即可访问完整的产品文档。
2. 矩阵和幻方矩阵
关于矩阵
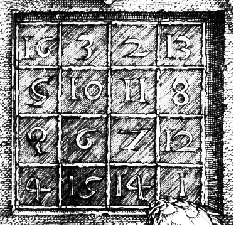
在 MATLAB® 环境中,矩阵是由数字组成的矩形数组。有时,1×1 矩阵(即标量)和只包含一行或一列的矩阵(即向量)会附加特殊含义。MATLAB 采用其他方法来存储数值数据和非数值数据,但刚开始时,通常最好将一切内容都视为矩阵。MATLAB 旨在尽可能简化运算。其他编程语言一次只能处理一个数字,而 MATLAB 允许您轻松快捷地处理整个矩阵。本手册中使用的有效示例矩阵摘自德国艺术家和业余数学家 Albrecht Dürer 在文艺复兴时期的雕刻 Melencolia I。

这幅图布满了数学符号,通过仔细观察,您会发现右上角有一个矩阵。此矩阵称为幻方矩阵,在 Dürer 所处的时代,此幻方矩阵被视为富有真正的神秘性质。它具有某些值得让人深究的迷人特征。
输入矩阵
开始学习 MATLAB 的最佳方法是了解如何处理矩阵。启动 MATLAB 并按照每个示例操作。
您可以采用多种不同方法在 MATLAB 中输入矩阵:
- 输入元素的明确列表。
- 从外部数据文件加载矩阵。
- 使用内置函数生成矩阵。
- 使用您自己的函数创建矩阵,并将其保存在文件中。
首先,以元素列表的形式输入丢勒的矩阵。您只需遵循一些基本约定:
- 使用空格或逗号分隔行的元素。
- 使用分号
;表示每行末尾。 - 使用方括号
[ ]将整个元素列表括起来。
要输入丢勒矩阵,只需在命令行窗口中键入即可
1 | A = [16 3 2 13; 5 10 11 8; 9 6 7 12; 4 15 14 1] |
MATLAB 显示刚才您输入的矩阵:
1 | A = |
此矩阵与雕刻中的数字一致。输入矩阵之后,MATLAB 工作区会自动记住此矩阵。您可以将其简称为 A。现在,您已经在工作区中输入 A,让我们看看它为什么如此有趣吧。它有什么神奇的地方呢?
矩阵求和、转置和对角矩阵
您可能已经注意到,幻方矩阵的特殊属性与元素的不同求和方法相关。如果沿任何行或列求和,或者沿两条主对角线中的任意一条求和,您将始终得到相同数字。让我们使用 MATLAB 来验证这一点。尝试的第一个语句是
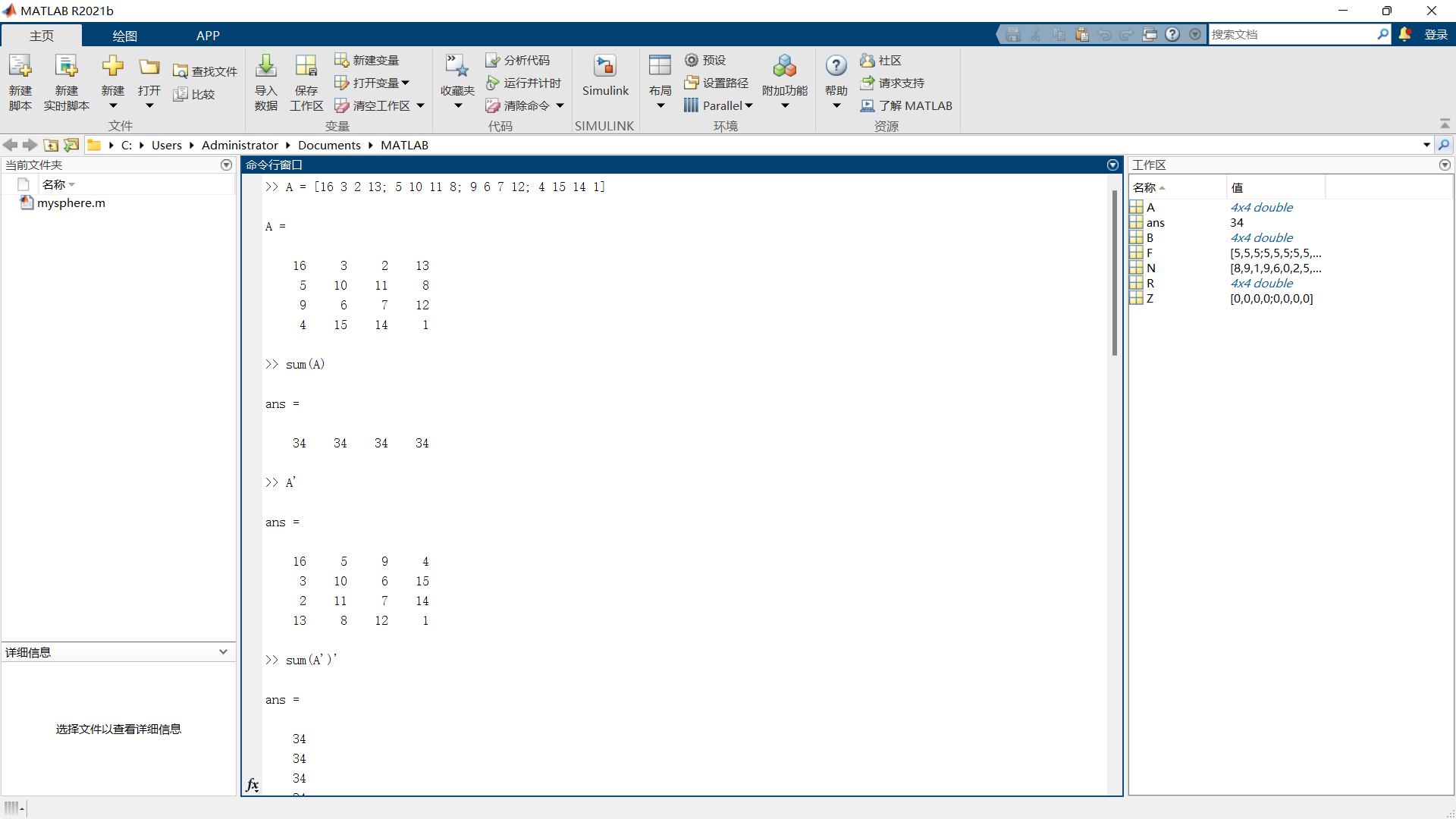
1 | sum(A) |
MATLAB 返回的结果为
1 | ans = |
如果未指定输出变量,MATLAB 将使用变量 ans(answer 的缩略形式)来存储计算结果。您已经计算包含 A 的列总和的行向量。每个列的总和都相同,即幻数和 34。
行总和如何处理?MATLAB 会优先处理矩阵的列,因此获取行总和的一种方法是转置矩阵,计算转置的列总和,然后转置结果。
MATLAB 具有两个转置运算符。撇号运算符(例如,A')执行复共轭转置。它会围绕主对角线翻转矩阵,并且还会更改矩阵的任何复数元素的虚部符号。点撇号运算符 (A.') 转置矩阵,但不会影响复数元素的符号。对于包含所有实数元素的矩阵,这两个运算符返回相同结果。
因此
1 | A' |
生成
1 | ans = |
而
1 | sum(A')' |
生成包含行总和的列向量
1 | ans = |
有关避免双重转置的其他方法,请在 sum 函数中使用维度参数:
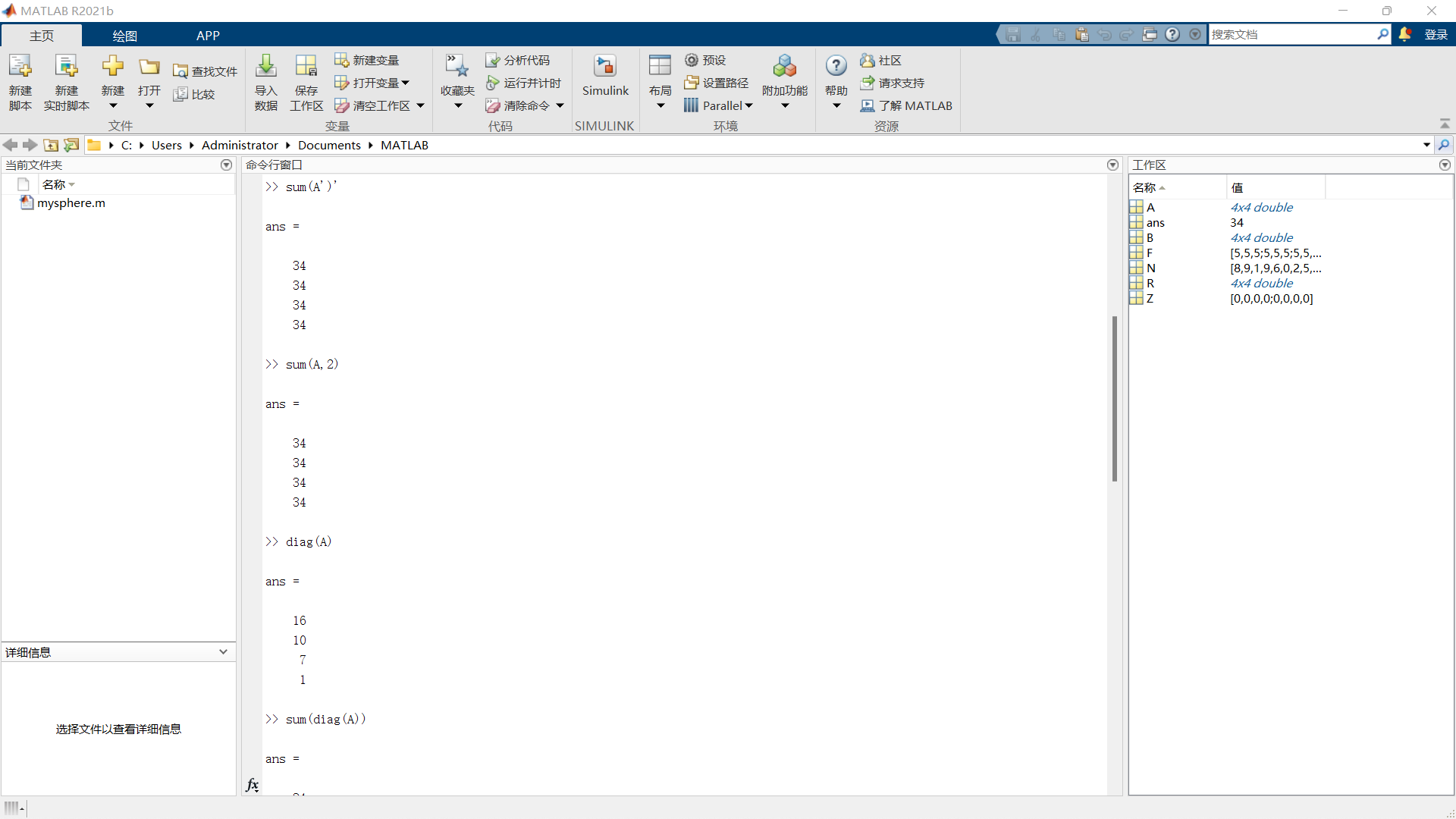
1 | sum(A,2) |
生成
1 | ans = |
使用 sum 和 diag 函数可以获取主对角线上的元素的总和:
1 | diag(A) |
生成
1 | ans = |
而
1 | sum(diag(A)) |
生成
1 | ans = |
从数学上讲,另一条对角线(即所谓的反对角线)并不是十分重要,因此 MATLAB 没有对此提供现成的函数。但原本用于图形的函数 fliplr 可以从左往右地翻转矩阵:
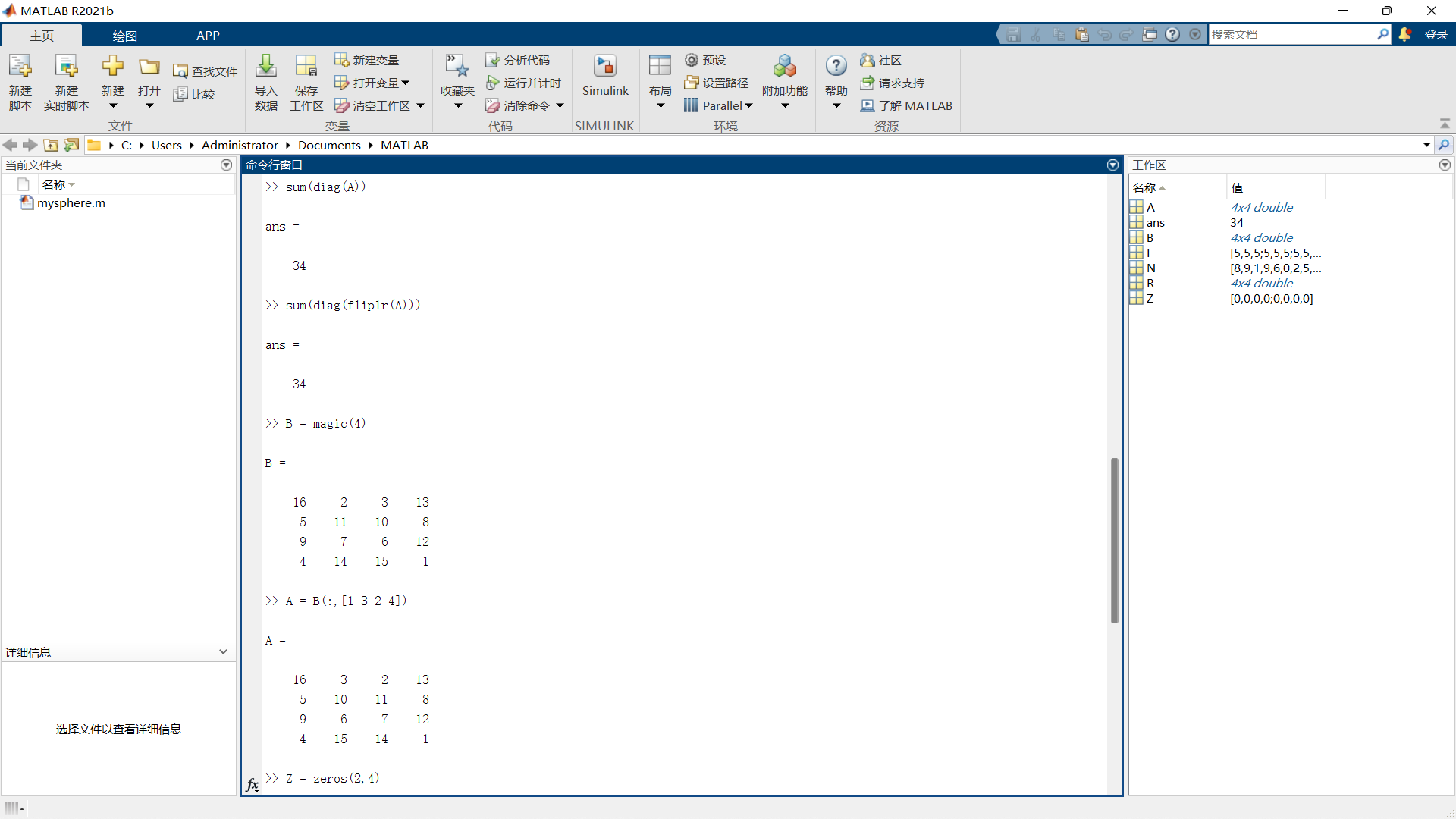
1 | sum(diag(fliplr(A))) |
1 | ans = |
您已经验证丢勒雕刻中的矩阵确实是一个幻方矩阵,同时在验证过程中,您已经尝试了几个 MATLAB 矩阵运算。下面各部分继续使用此矩阵来演示 MATLAB 的其他功能。
magic 函数
MATLAB 实际包含一个内置函数,该函数可创建几乎任意大小的幻方矩阵。此函数称为 magic 也就不足为奇了:
1 | B = magic(4) |
此矩阵几乎与丢勒雕刻中的矩阵相同,并且具有所有相同的“神奇”性质;唯一区别在于交换了中间两列。
您可以交换 B 的中间两列,使其看起来像丢勒 A。针对 B 中的每一行,按照指定顺序(1、3、2、4)对列进行重新排列:
1 | A = B(:,[1 3 2 4]) |
生成矩阵
MATLAB 软件提供了四个用于生成基本矩阵的函数。
zeros |
全部为零 |
|---|---|
ones |
全部为 1 |
rand |
均匀分布的随机元素 |
randn |
正态分布的随机元素 |
下面给出了一些示例:
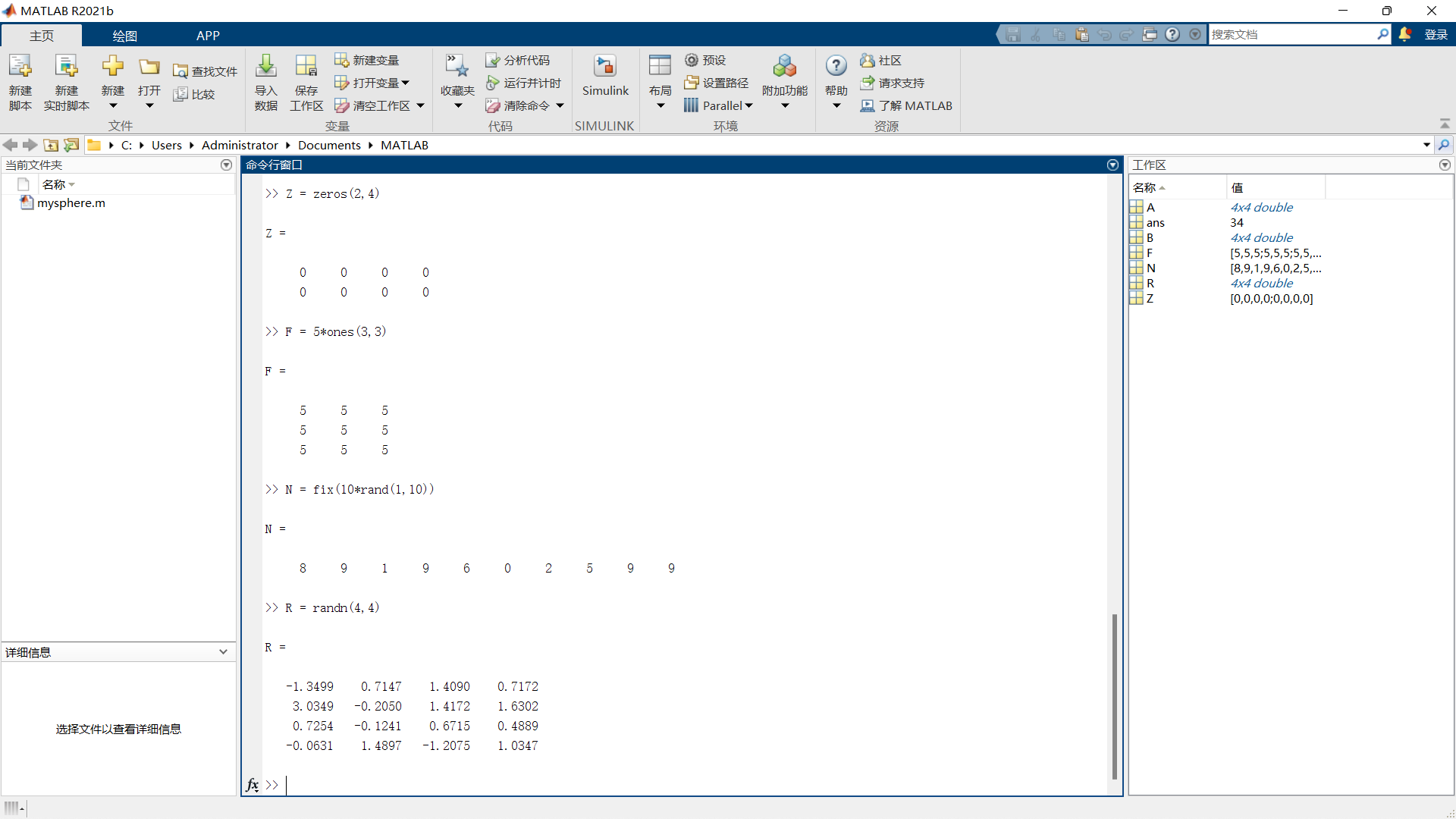
1 | Z = zeros(2,4) |
1 | F = 5*ones(3,3) |
1 | N = fix(10*rand(1,10)) |
1 | R = randn(4,4) |
3. 表达式
变量
与大多数其他编程语言一样,MATLAB® 语言提供数学表达式,但与大多数编程语言不同的是,这些表达式涉及整个矩阵。
MATLAB 不需要任何类型声明或维度说明。当 MATLAB 遇到新的变量名称时,它会自动创建变量,并分配适当大小的存储。如果此变量已存在,MATLAB 会更改其内容,并根据需要分配新存储。例如,
1 | num_students = 25 |
创建一个名为 num_students 的 1×1 矩阵,并将值 25 存储在该矩阵的单一元素中。要查看分配给任何变量的矩阵,只需输入变量名称即可。
变量名称包括一个字母,后面可以跟随任意数目的字母、数字或下划线。MATLAB 区分大小写;它可以区分大写和小写字母。A 和 a 不是相同变量。
尽管变量名称可以为任意长度,MATLAB 仅使用名称的前 N 个字符(其中 N 是函数 namelengthmax 返回的数字),并忽略其余字符。因此,很重要的一点是,应使每个变量名称的前 N 个字符保持唯一,以便 MATLAB 能够区分变量。
1 | N = namelengthmax |
数字
MATLAB 使用传统的十进制记数法以及可选的小数点和前导加号或减号来表示数字。科学记数法使用字母 e 来指定 10 次方的缩放因子。虚数使用 i 或 j 作为后缀。下面给出了合法数字的一些示例:
1 | 3 -99 0.0001 |
MATLAB 使用 IEEE® 浮点标准规定的 long 格式在内部存储所有数字。浮点数的有限精度约为 16 位有效小数位数,有限范围约为 10-308 至 10+308。
以双精度格式表示的数字的最大精度为 52 位。任何需要 52 位以上的双精度数字都会损失一定精度。例如,下面的代码因截断而将两个不相等的值显示为相等:
1 | x = 36028797018963968; |
整数的可用精度为 8 位、16 位、32 位和 64 位。将相同数字存储为 64 位整数会保留精度:
1 | x = uint64(36028797018963968); |
MATLAB 软件存储复数的实部和虚部。该软件根据上下文采用不同方法来处理各个部分的量值。例如,sort 函数根据量值进行排序,如果量值相等,则根据相位角度排序。
1 | sort([3+4i, 4+3i]) |
这是由相位角度所致:
1 | angle(3+4i) |
“等于”关系运算符 == 要求实部和虚部相等。其他二进制关系运算符 >、<、>= 和 <= 忽略数字的虚部,而仅考虑实部。
矩阵运算符
表达式使用大家熟悉的算术运算符和优先法则。
+ |
加法 |
|---|---|
| - | 减法 |
* |
乘法 |
/ |
除法 |
\ |
左除 |
^ |
幂 |
' |
复共轭转置 |
( ) |
指定计算顺序 |
数组运算符
如果矩阵不用于线性代数运算,则成为二维数值数组。数组的算术运算按元素执行。这意味着,加法和减法运算对数组和矩阵都是相同的,但乘法运算不相同。MATLAB 的乘法数组运算表示法中包含点,也就是小数点。
运算符列表包括
+ |
加法 |
|---|---|
- |
减法 |
.* |
逐元素乘法 |
./ |
逐元素除法 |
.\ |
逐元素左除 |
.^ |
逐元素幂 |
.' |
非共轭数组转置 |
如果使用数组乘法将丢勒的幻方矩阵自乘
1 | A.*A |
则会生成一个数组,该数组包含介于 1 至 16 之间的整数的平方,并且以不常见的顺序排列:
1 | ans = |
构建表
数组运算对构建表非常有用。假定 n 为列向量
1 | n = (0:9)'; |
然后,
1 | pows = [n n.^2 2.^n] |
构建一个平方和 2 次幂的表:
1 | pows = |
初等数学函数逐元素处理数组元素。因此
1 | format short g |
构建一个对数表。
1 | logs = |
函数
MATLAB 提供了大量标准初等数学函数,包括 abs、sqrt、exp 和 sin。生成负数的平方根或对数不会导致错误;系统会自动生成相应的复数结果。MATLAB 还提供了许多其他高等数学函数,包括贝塞尔函数和 gamma 函数。其中的大多数函数都接受复数参数。有关初等数学函数的列表,请键入
1 | help elfun |
有关更多高等数学函数和矩阵函数的列表,请键入
1 | help specfun |
某些函数(例如,sqrt 和 sin)是内置函数。内置函数是 MATLAB 核心的一部分,因此这些函数非常高效,但计算详细信息是不可访问的。其他函数使用 MATLAB 编程语言实现,因此可以访问其计算详细信息。
内置函数与其他函数之间存在一些差异。例如,对于内置函数,您看不到代码。对于其他函数,您可以看到代码,甚至可以根据需要修改代码。
一些特殊函数提供了有用的常量值。
pi |
3.14159265… |
|---|---|
i |
虚数单位 √−1 |
j |
与 i 相同 |
eps |
浮点相对精度 ε=2−52 |
realmin |
最小浮点数 2−1022 |
realmax |
最大浮点数 (2−ε)21023 |
Inf |
无穷 |
NaN |
非数字 |
通过将非零值除以零或计算明确定义的溢出(即超过 realmax)的数学表达式,会生成无穷值。通过尝试计算 0/0 或 Inf-Inf 等没有明确定义的数值的表达式,会生成非数字。
函数名称不会保留。您可以使用如下新变量覆盖任何函数名称
1 | eps = 1.e-6 |
并在后续计算中使用该值。可以使用以下命令恢复原始函数
1 | clear eps |
表达式示例
您已经学习了 MATLAB 表达式的几个示例。下面是一些其他示例及生成的值:
1 | rho = (1+sqrt(5))/2 |
1 | a = abs(3+4i) |
1 | z = sqrt(besselk(4/3,rho-i)) |
1 | huge = exp(log(realmax)) |
1 | toobig = pi*huge |





