`一.简介`

本系列是用来分享在洛谷，LeetCode的有趣的题目，使用Java编写且代码解释以注释为主。

本篇涉及：哈希表，双指针

`二.题目`

1. 无重复字符的最长子串

题目描述：

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

输入输出样例：

示例 1:

1
2
3

>输入: s = "abcabcbb"
>输出: 3 
>解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

1
2
3

输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 3:

输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
  请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

提示:

0 <= s.length <= 5 * 104
s 由英文字母、数字、符号和空格组成

方法一：滑动窗口

我们使用两个指针表示字符串中的某个子串（或窗口）的左右边界
在每一步的操作中，我们会将左指针向右移动一格，表示 我们开始枚举下一个字符作为起始位置
然后我们可以不断地向右移动右指针，但需要保证这两个指针对应的子串中没有重复的字符（使用哈希表）。
在移动结束后，这个子串就对应着 以左指针开始的，不包含重复字符的最长子串。我们记录下这个子串的长度；
将左指针的位置指向右指针的位置，右指针继续右移开始下一轮查找。

在枚举结束后，我们找到的最长的子串的长度即为答案。

/**
 * 我们还需要使用一种数据结构来判断 是否有重复的字符，常用的数据结构为哈希集合
 * 在左指针向右移动的时候，我们从哈希集合中移除一个字符，在右指针向右移动的时候，我们往哈希集合中添加一个字符。
 *
 * 复杂度分析:
 * 时间复杂度：O(N)，其中 N 是字符串的长度。左指针和右指针分别会遍历整个字符串一次。
 * 空间复杂度：O(∣Σ∣)，其中 Σ 表示字符集（即字符串中可以出现的字符），∣Σ∣ 表示字符集的大小。
 * 在本题中没有明确说明字符集，因此可以默认为所有 ASCII 码在 [0, 128)[0,128) 内的字符，
 * 即 ∣Σ∣=128。我们需要用到哈希集合来存储出现过的字符，而字符最多有 ∣Σ∣ 个，因此空间复杂度为 O(∣Σ∣)。
 *
 */
class Solution {
    public int lengthOfLongestSubstring(String s) {
        if (s.length() == 0) return 0;
        HashMap<Character, Integer> map = new HashMap<Character, Integer>();
        int max = 0;//最长子串长度
        int left = 0;//滑动窗口左下标，i相当于滑动窗口右下标
        for (int i = 0; i < s.length(); i++) {
            //charAt() 方法用于返回指定索引处的字符。索引范围为从 0 到 length() - 1。
            if (map.containsKey(s.charAt(i))) {
                //map.get():返回字符所对应的索引，当发现重复元素时，窗口左指针右移，直到不重复为止
                //map.get('a')=0,因为map中只有第一个a的下标，然后更新left指针到原来left的的下一位
                left = Math.max(left, map.get(s.charAt(i)) + 1);
            }
            //更新map中a映射的下标
            map.put(s.charAt(i), i);
            //比较两个参数的大小，返回较大的那个
            max = Math.max(max, i - left + 1);
        }
        return max;
    }
}

2. 盛最多水的容器

题目描述：

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。

说明：你不能倾斜容器。

输入输出样例：

示例 1:

1
2
3

>输入：[1,8,6,2,5,4,8,3,7]
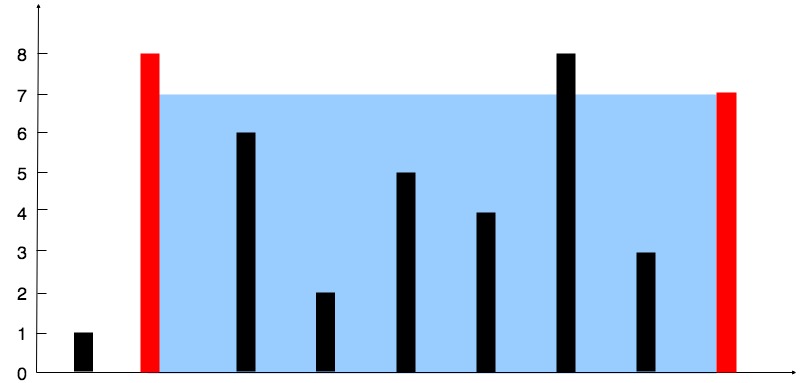
>输出：49 
>解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2:

1 2	输入：height = [1,1] 输出：1

提示:

n == height.length
2 <= n <= 105
0 <= height[i] <= 104

方法一：双指针

设两指针 i , j ，指向的水槽板高度分别为 h[i] , h[j] ，此状态下水槽面积为 S(i, j) 。由于可容纳水的高度由两板中的短板决定，因此可得如下 面积公式： S(i, j) = min(h[i], h[j]) × (j - i)

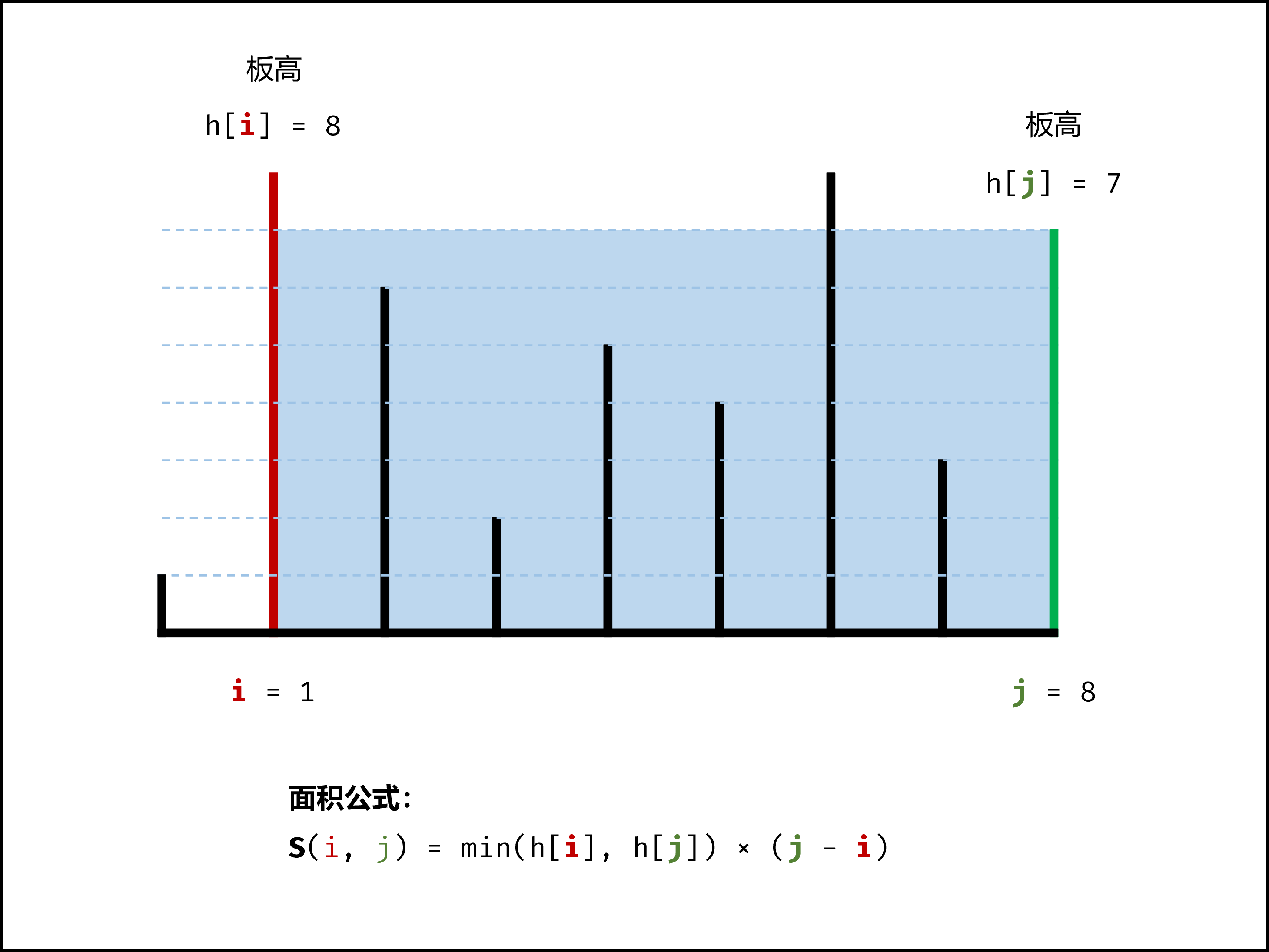
在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽底边宽度 -1−1 变短：

若向内 移动短板 ，水槽的短板 min(h[i], h[j]) 可能变大，因此下个水槽的面积 可能增大 。
若向内 移动长板 ，水槽的短板 min(h[i], h[j]) 不变或变小，因此下个水槽的面积 一定变小 。

因此，初始化双指针分列水槽左右两端，循环每轮将短板向内移动一格，并更新面积最大值，直到两指针相遇时跳出；即可获得最大面积。

/**
 * 1. 初始化： 双指针 i , j 分列水槽左右两端；
 * 2. 循环收窄： 直至双指针相遇时跳出；
 * 1. 选定两板高度中的短板，向中间收窄一格；
 * 2. 更新面积最大值 res ；
 * 3. 返回值： 返回面积最大值 res 即可；
 *
 * 复杂度分析：
 * 时间复杂度 O(N) ： 双指针遍历一次底边宽度 N。
 * 空间复杂度 O(1)： 变量 i , j , res 使用常数额外空间。
 */

public class Problem11 {
    public int maxArea(int[] height) {
        // 初始化： 双指针 i , j 分列水槽左右两端；
        int i = 0, j = height.length - 1, res = 0;
        // 循环收窄： 直至双指针相遇时跳出；
        while (i < j) {
            // 选定两板高度中的短板，向中间收窄一格；
            res = height[i] < height[j] ?
                    Math.max(res, (j - i) * height[i++]) :
                    Math.max(res, (j - i) * height[j--]);
        }
        return res;
    }
}